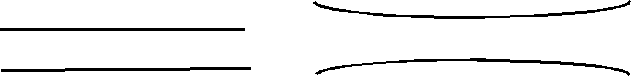
α + β + γ = 180
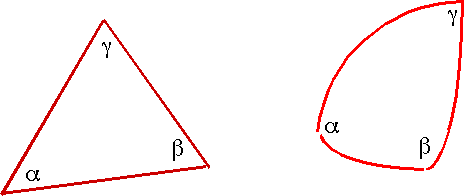
Note we have carefully avoided saying what we mean by a curved space
If you take the example of the 2-D curved surface of the Earth, this is embedded in a 3-D space. Hence If a massive body curves space, it almost implies extra dimensions. In fact we can carry out tests to decide if we live in a "normal" 3-D space (Euclidean) e.g.
| parallel lines | 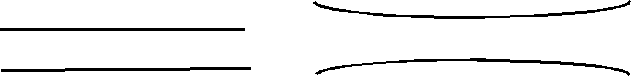 |
angles of a triangle add up to 1800 α + β + γ = 180 |
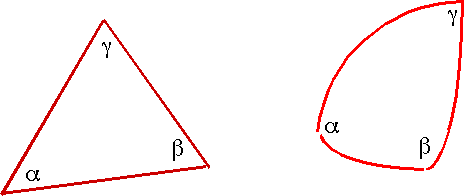 |
C = 2πaIn fact,
C = 2πx = 2πRsin(a/R) = 2πa(1-a2/6R2)
i.e. by measuring the circ. of large circles, we can determine if we live in a curved space. These are experiments that we can almost do. (Gauss tried the 2nd!). We can measure the curvature k ≡ 1/R2; (a physicist would say we are measuring distant-dependence corrections to π!)
Can also have negative curvature K<0.
How do we know analytically if we are in a curved space?
| e.g. a cylinder will satisfy (most) Euclidean geometry. We can "unwrap" a cylinder into a flat surface, we can't unwrap a sphere without distorting it. |  |
| Note that on a cylinder we can have closed and open geodesics, in flat plane can only have open geodesics | 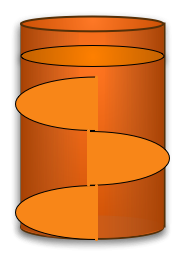 |
| Can only interpret this in "slices" |  |
| We can find the area and radius of an r-sphere:$$ \color{red}{ a\left( r \right) = \int_0^a {ds} = \int_0^r {\frac{{dr}}{{\left( {1 - Kr^2 } \right)^{1/2} }}} = \frac{1}{{\sqrt K }}\sin ^{ - 1} \left( {r\sqrt K } \right)} $$ | 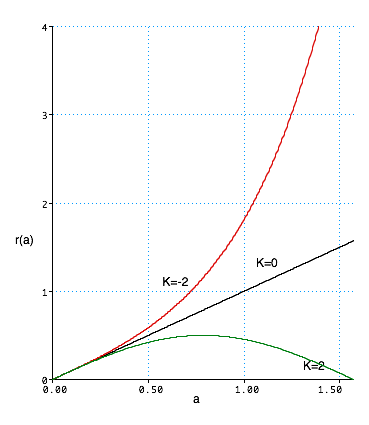 |
First step is curvature due to a massive body $$ \color{red}{ K\left( r \right) = - \frac{{GM}}{{c^2 r^3 }}} $$ (Dimensional argument, but also can show this reduces to Newton's laws.
| A ball thrown up near the earth's surface will lose energy. | 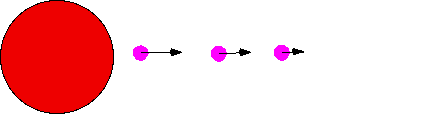 |
| (Confirmed by Rebka-Pound using Mossbauer techniques in 1960. An atom is a good clock: | 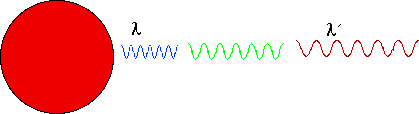 |
This is another consequence of the equivalence principle: confirmed in numerous experiments over the last 40 years. Implies that clocks run slow in gravitational fields $$ \color{red}{ t' = \frac{t}{{\left( {1 - \frac{{2GM}}{{c^2 r}}} \right)^{1/2} }}} $$ Then Schwarzchild metric $$ \color{red}{ g_{\mu \nu } = \left[ {\begin{array}{*{20}c} {1 - \frac{{2GM}}{{c^2 r}}} & 0 & 0 & 0 \\ 0 & { - \frac{1}{{c^2 \left( {1 - \frac{{2GM}}{{c^2 r}}} \right)}}} & 0 & 0 \\ 0 & 0 & { - \frac{{r^2 }}{{c^2 }}} & 0 \\ 0 & 0 & 0 & { - \frac{{r^2 \sin ^2 \left( \theta \right)}}{{c^2 }}} \\ \end{array}} \right]} $$ (can find g11 by variant of last argument: to find g00 need to have the metric independent of time even though. clocks run slow. Schwarzchild radius R = 2GM/c2 is where metric becomes singular.
in particular, if
r = 2GM
c2
then t = ∞: i.e. if I watch a clock at the Schwarzchild radius, it appears to have stopped.
From this can get all the classic tests of GR (see Clifford Will).
| What does this look like? As long as speeds are small, exactly the same as Newton (Ha!), but if velocities are "large" then the force gets changed
Fact that orbits are closed is "coincidence" not true for any potentials except r2, 1/r and 1/r2 Hence get "rosette" orbits. |
 |
Much less dramatic in practice: perihelion (closest approach to sun) of Mercury advances by 43" arc/century
And light gets does bent: this is a very large cluster of galaxies, which acts as a very large (and rather bad!) lens. It produces several images of a much more distant galaxy
A final consequence:
|
 |
Differences: that
Hence (well, more or less hence!) it requires a large amount of mass to produce a grav. wave, and a large amount to see one: e.g need to detect motions of << atomic radius in a one ton sapphire crystal.
History:Hulse and Taylor: Binary Pulsar PSR1913+16 discovered 1974. Like all pulsars, emits very regular radio pulse every 59 ms. (Frequency is 16.940 539 184 253 Hz: i.e. is better known than atomic clocks)
This consists of two neutron stars, in orbit 106 km in radius, with period of hours. Change in frequency allows orbit to be calculated exactly, and can measure..
Rate of precession = 4.22662 0/yr (i.e. 30,000x that of Mercury)
and that pulsar is losing energy, by gravitational radiation (mass~1.4 M0, and accns are large)
| Decrease of the orbital period P (about 7h 45 min) of the binary pulsar PSR B1913+16, measured by the successive shifts T(t) of the crossing times at periastron; the continuous curve corresponds to $$ \color{red}{ T(t) = \frac{{t^2 }}{{2P}}\frac{{dP}}{{dt}}} $$ given by the general relativity (reaction to the gravitational waves emission) | 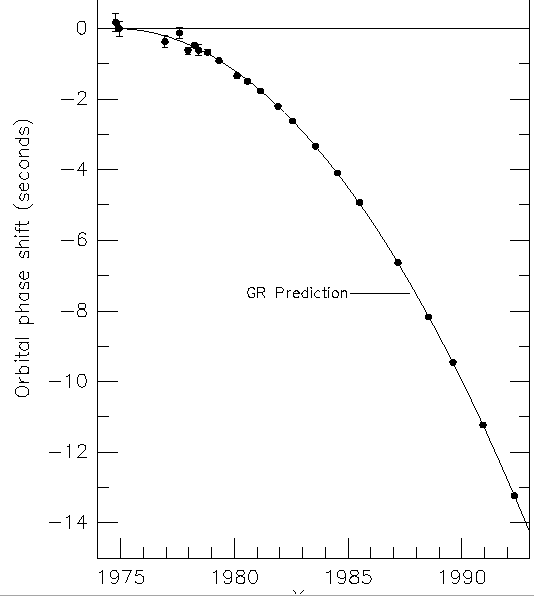 Reference: Taylor J.H. 1993, Testing relativistic gravity with binary and millisecond pulsars, in General Relativity and Gravitation 1992, eds. R.J. Gleiser, C.N. Kozameh, O.M. Moreschi. Institute of Physics Publishing (Bristol). |
Hence 1993 Nobel Prize
So we conclude that Relativity (Special and General) works because